Batystuta Rocha

Copyright OpenScience © 2018.

- by Batystuta Rocha, 15 Out, 2018.

Obrigado: Profa. Edith Beatriz pelo apoio ao conhecimento, muito obrigado.
Versão 1.0 outubro 2018.

Este é o primeiro notebook do material FluidoPython, para Escoamento Potencial. Se você não estiver familiarizado com a computação numérica usando o Python, primeiro estude as ferramentas científica em Python, recomendada como "lição zero" deste material.

Você pode ler e acompanhar este caderno on-line, enquanto digita o código em seu próprio bloco de anotações Jupyter limpo ou em um arquivo ".py" no seu editor Python favorito. De qualquer maneira, certifique-se de experimentar os códigos e escrever suas próprias versões e assim ampliando o seu conhecimento!

A mecânica dos fluidos é um tema excitante e fascinante, com aplicações práticas ilimitadas que variam de sistema biológicos microscópicos a automóveis, aviões e propulsão de aeronaves. Contudo, ela é também, historicamente, um dos assuntos mais desafiadores para os estudantes universitários. Dessa maneira, é importantíssimo o uso extensivo de imagens como um instrumento de aprendizagem que ajuda o aluno a entender a matéria.

A base teórica para a aerodinâmica clássica é a teoria do fluxo potencial, um aparato matemático que foi o sangue vital da aerodinâmica através de seu crescimento até a maturidade durante a maior parte do século XX.

Tudo começa com algumas simplificações:

• o fluxo é constante;
• a velocidade permanece menor que a velocidade do som (fluxo incompressível);
• o fluido não tem atrito interno, isto é, é invíscido; e
• não tem vorticidade (partículas fluidas não estão girando).

Isso soa como muitas simplificações, não é? Acontece que uma grande parte da aerodinâmica pode ser aproximada dessa maneira! Efeitos viscosos são normalmente confinados a uma camada limite muito fina (e podemos corrigir a teoria do potencial para modelar), e muitos fluxos são efetivamente irrotacionais (exceto pontos isolados, linhas ou folhas). E, finalmente, a maioria dos aplicativos nos quais estamos interessados permanece sub-sônica.

A teoria do fluxo de potencial tem uma qualidade matemática muito agradável: é linear . Isso significa que o princípio da superposição se aplica, e podemos construir novas soluções adicionando soluções conhecidas.

Lembre-se que, se os efeitos viscosos são desprezados, os escoamentos a baixas velocidades são irrotacionais, $\bigtriangledown \times V = 0$, existindo o potencial de velocidades $\phi$ tal que

$$ \mathrm{V} = \bigtriangledown \phi $$ $$ \mathit{u} = \frac{\partial \phi }{\partial x} \>\>\>\> \mathit{v} = \frac{\partial \phi }{\partial y} \>\>\>\> \mathit{w} = \frac{\partial \phi }{\partial z} $$

A equação da continuidade, $\bigtriangledown V = 0$, reduz-se à equação de Laplace para $\phi$:

$$ \bigtriangledown ^{2} \phi = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} + \frac{\partial^2 \phi}{\partial z^2} = 0 $$

Relembre que, se um escoamento é descrito por apenas duas coordenadas, também existe a função corrente $\psi$ como uma opção de abordagem. Para escoamentos incompressíveis planos, em coordenadas $\mathit{xy}$, a forma correta é:

$$ \mathit{u} = \frac{\partial \psi }{\partial x} \>\>\>\>\> \mathit{v} = - \frac{\partial \psi }{\partial y} $$

A condição de irrotacionalidade também reduz-se à equação de Laplace para $\psi$:

$$ 2\omega _{z} = 0 = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} = \frac{\partial }{\partial x}\left ( -\frac{\partial \psi}{\partial x} \right ) - \frac{\partial }{\partial y}\left ( \frac{\partial \psi}{\partial y} \right ) $$ $$ \frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} = 0 $$

Para as aplicações deste material, podemos calcular tanto o $\phi$ como $\psi$, ou ambas, e a solução correspondente será uma rede de escoamento ortogonal, como na figura abaixo.

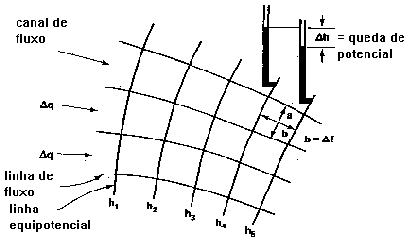
Muitas soluções são convenientemente expressas em coordenadas polares $(r,\theta)$. Os componentes de velocidade e as relações diferenciais para as funções $\phi$ e $\psi$ são alterados para as seguintes formas:

$$ v_{r} = \frac{\partial \phi}{\partial r} = \frac{1}{r} \frac{\partial \psi}{\partial \theta} \>\>\>\>\> v_{\theta} = \frac{1}{r} \frac{\partial \phi}{\partial \theta} = - \frac{\partial \psi}{\partial r} $$

A equação de Laplace assume a seguinte forma:

$$ \frac{1}{r} \frac{\partial }{\partial r} \left ( r \frac{\partial \phi}{\partial r} \right ) + \frac{1}{r^{2}} \frac{\partial^2 \phi}{\partial \theta^{2}} = 0 $$

Para $\psi(r,\theta)$, a mesma equação vale exatamente em termos de coordenadas polares:

$$ \frac{1}{r} \frac{\partial }{\partial r} \left ( r \frac{\partial \psi}{\partial r} \right ) + \frac{1}{r^{2}} \frac{\partial^2 \psi}{\partial \theta^{2}} = 0 $$

Um aspecto intrigante do escoamento potencial sem superfície livre é que tanto as equações governantes, equação de Laplace para $\psi$ e $\phi$ não contêm parâmetros. Logo, as soluções são puramente geométricas, dependendo apenas do formato do corpo, da orientação da corrente livre e - surpreendentemente - da posição do ponto de estagnação traseiro. Não há número de Reynolds, Froude ou Mach para complicar a semelhança dinâmica. Os escoamentos não viscosos são cinematicamente semelhantes sem parâmetros adicionais.