Batystuta Rocha

Copyright OpenScience © 2018.

- by Batystuta Rocha, 15 Out, 2018.

Obrigado: Profa. Edith Beatriz pelo apoio ao conhecimento, muito obrigado.
Versão 1.0 outubro 2018.

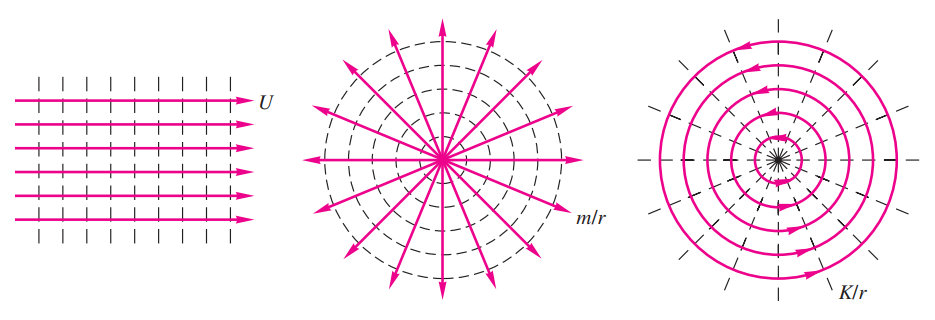
Este tópico apresento um estudo introdutório detalhado dos escoamentos incompressíveis não viscosos, especialmente aqueles que possuem ambas as funções, corrente e potencial de velocidade. Muitas soluções empregam o princípio da superposição, de modo que destaquei esse tipo de solução em um único módulo para melhor detalhe. Aqui vamos começar com os três escoamentos elementares, ilustrados na figura abaixo: (a) uma corrente uniforme em certa direção, (b) uma linha de fonte / sumidouro na origem e (c) uma linha de vórtice na origem.

1.1. Corrente uniforme em certa direção ¶

O escoamento elementar mais simples em que podemos pensar é uma corrente uniforme

$$ V = iU, $$

como o primeiro esquema da figura acima, movendo-se com velocidade constante U na direção $(x)$ (da esquerda para direita). E que tem tanto uma função corrente como uma função potencial de velocidades, as quais podem ser encontradas da seguinte maneira:

$$ u = U = \frac{\partial \phi}{\partial x} = \frac{\partial \psi}{\partial y} \>\>\>\>\> v = 0 = \frac{\partial \phi}{\partial y} = -\frac{\partial \psi}{\partial x} $$

Integrando a primeira dessas equações com relação a $(x)$ e depois diferenciando o resultado em relação a $(y)$, geramos uma expressão para a função potencial de velocidade para uma corrente uniforme:

$$ \phi = Ux + f(y) \>\>\> --> \>\>\> v = \frac{\partial \phi}{\partial y} = f^{'}(y) = 0 \>\>\> --> \>\>\> f(y) = constante $$

A constante é arbitrária, já que as componentes da velocidade são sempre derivadas de $\psi$. Fazemos a constante igual a zero, sabendo que podemos sempre adicionar uma constante arbitrária mais tarde se desejarmos. Portanto:

Função potencial de velocidade para uma corrente uniforme: $\phi = Ux$

De maneira similar geramos uma expressão para a função de corrente para esse escoamento irrotacional planar elementar:

Função de corrente para uma corrente uniforme: $\psi = Uy$

As linhas de corrente são linhas retas horizontais $(y = const)$, e as linhas equipotenciais são verticais $(x = const)$, ou seja, ortogonais às linhas de corrente, como se esperava.

Muitas vezes é conveniente expressar a função de corrente e a função potencial de velocidade em coordenadas cilíndricas em vez de coordenadas cartesianas, particularmente quando formos sobrepor uma corrente uniforme a algum outro escoamento irrotacional planar. As relações de conversão são obtidas da geometria da figura abaixo:

$$ x = r \cos(\theta) \>\>\>\> y = r \sin(\theta) \>\>\>\> r = \sqrt(x^{3} + y^{3}) $$

Com as equações acima e um pouco de trigonometria, deduzimos relações para $u$ e $v$ em termos de coordenadas cilíndricas:

$$ u = [u_{r} \cos(\theta) - u_{\theta} \sin(\theta)] \>\>\>\>\> v = [u_{r} \sin(\theta) - u_{\theta} \cos(\theta)] $$

Em coordenadas cilíndricas, a função $\psi$ e $\phi$ tornam-se

$$ \phi = U \> r \cos(\theta) \>\>\>\> \psi = U \> r \sin(\theta) $$

1.2. Linha de fonte ou sumidouro na origem ¶

Nosso segundo escoamento elementar é uma linha de fonte localizada na origem do plano $(xy)$, com a própria linha coincidindo com o eixo $(z)$. Suponha que o eixo $(z)$ seja uma espécie de tubo distribuidor bem fino, por meio do qual o fluido seria emitido uniformemente a uma vazão total $(Q)$ ao longo de seu comprimento $(b)$. Observando o plano $(xy)$, veríamos um escoamento radial cilíndrico para fora, ou fonte, como esboça o segundo esquema da figura apresentada. As coordenadas polares no plano são adequadas, pois não há velocidade circunferencial e a qualquer distância radial $(r)$ da linha de fonte, a componente radial da velocidade, $(u_{r})$ pode ser determinada aplicando-se o princípio da conservação da massa. Isto é, toda a vazão em volume por unidade de profundidade da linha de fonte deve passar através do círculo definido pelo raio $(r)$ . Assim:

$$ \frac{Q}{b} = 2\pi r u_{r} \>\>\>\>\> u_{r} = \frac {Q/b}{2\pi r} $$ $$ u_{r} = \frac {Q/b}{2\pi r} = \frac{m}{r}=\frac{1}{r}\frac{\partial \psi}{\partial \theta} = \frac{\partial \phi}{\partial r} \>\>\>\>\> u_{\theta} = 0 = -\frac{\partial \psi}{\partial r} = \frac{1}{r} \frac{\partial \phi}{\partial \theta} $$

Usando coordenadas cilíndricas no termo da velocidade radial, e também reconhecendo que $(u_{\theta})$ é zero em todos os pontos e que $m = Q/(2\pi b)$ é uma constante, positiva para uma fonte, negativa para um sumidouro. Integrando e descartando outra vez as constantes de integração, obtemos as funções apropriadas para esse escoamento radial simples:

$$ \psi = m \theta \>\>\>\>\> \phi = m \ln r $$

Como mostrado no segundo esquema, as linhas de corrente são raios $( \theta \>constante)$, e as linhas equipotenciais são círculos $( r \>constante)$. E as linhas de corrente e linhas equipotenciais são mutuamente ortogonais em todos os pontos exceto na origem, que é um ponto singular.

Em situações nas quais gostaríamos de colocar uma linha de fonte ou sumidouro em algum outro lugar que não seja na origem, devemos transformar as equações perigosamente, rsrsrs, na verdade, cuidadosamente. Para entender essa transformação com mais detalhes recomendo a leitura do livro Mecânica dos Fluidos Fundamentos e Aplicações, Çengel e Cimbala. É necessário um pouco de trigonometria para transformar as equações, e assim obteremos as funções em coordenadas cartesianas de uma fonte que está na localização absoluta (a,b):

$$ \psi = m \tan^{-1} \frac{y-b}{x-a} \>\>\>\>\>\> \phi = m \ln[\sqrt([x-a]^2 + [y-b]^2)] $$

1.3. Linha de vórtice irrotacional ¶

Nosso terceiro é uma linha de vórtice (bidimensional) e de caso simples no qual a linha está localizada na origem, tendo um movimento permanente puramente circulatório, e mais uma vez usamos coordenadas cilíndricos por conveniência, $u_{\theta} = f(r)$ apenas, e $u_{r} = 0$, que são:

$$ u_{r} =\frac{1}{r}\frac{\partial \psi}{\partial \theta} = \frac{\partial \phi}{\partial r} = 0 \>\>\>\>\> u_{\theta} = -\frac{\partial \psi}{\partial r} = \frac{1}{r} \frac{\partial \phi}{\partial \theta} = \frac {\Gamma}{2 \pi r} $$

onde $\Gamma$ é chamado de circulação ou intensidade do vórtice. Seguindo a convenção padrão da matemática, $\Gamma$ positivo representa vórtice no sentido anti-horário, enquanto $\Gamma$ negativo representa um vórtice no sentido horário.

Novamente, podemos integrar e determinar as funções apropriadas:

$$ \phi = \frac{\Gamma}{2 \pi} \>\theta \>\>\>\>\>\>\>\> \psi = -\frac{\Gamma}{2 \pi} \>ln(r) $$

Como mostra o último esquema, as linhas de corrente são círculos $( r \>constante)$ e as linhas equipotenciais são linhas radiais $( \theta \>constante)$. Observe a similaridade entre as Equações da linha de vórtice e linha de fonte, bah! é mesmo ... hehehehehe ... pois o vórtice livre é uma espécie de imagem reversa de uma fonte. O “vórtice de ralo”, que se forma quando água é drenada por um orifício no fundo de um tanque, é uma boa aproximação para o padrão de vórtice livre.

Em situações na quais gostaríamos de colocar o vórtice em algum outro lugar que não seja na origem, devemos transformar as equações conforme foi feita para uma linha de fonte. E assim obteremos as funções em coordenadas cartesianas de uma linha de vórtice que está na localização absoluta (a,b):

$$ \psi = -\frac{\Gamma}{2 \pi} \>ln[\sqrt([x-a]^2 + [y-b]^2)] \>\>\>\>\>\> \phi = \frac{\Gamma}{2 \pi} \> \tan^{-1} \frac{y-b}{x-a} $$