Batystuta Rocha

Copyright OpenScience © 2018.

- by Batystuta Rocha, 15 Out, 2018.

Obrigado: Profa. Edith Beatriz pelo apoio ao conhecimento, muito obrigado.
Versão 1.0 outubro 2018.

Podemos agora construir uma variedade de escoamentos potenciais interessantes, considerando as funções potencial e corrente de um escoamento uniforme, fontes, sumidouros e vórtices. A maioria dos resultados é clássica, é claro, necessitando apenas de um breve tratamento aqui. A superposição é válida porque as equações básicas das soluções elementares são lineares. Isso é verdade (e não é fake news ... hehehehehehe) porque a equação de Laplace é uma equação diferencial homogênea linear, a combinação linear de duas ou mais soluções da equação tem que ser também uma solução. Por exemplo, se $\phi_{1}$ e $\phi_{2}$ são soluções da equação de Laplace, então $A\phi_{1}$, $(A+\phi_{1})$, $(\phi_{1}+\phi_{2})$ e $(A\phi_{1}+B\phi_{2})$ também são soluções , onde $A$ e $B$ são constantes arbitrárias. Por extensão, poderíamos combinar várias soluções da equação de Laplace, e a combinação certamente é também uma solução. Se um escoamento é modelado pela soma de dois ou mais campos de escoamentos, por exemplo, uma fonte localizada em um escoamento de corrente uniforme, podemos simplesmente somar as funções potencial de velocidade destes dois escoamentos elementares (uniforme e fonte) em cada ponto para descrever o campo de escoamento combinado. Esse processo de somar duas ou mais soluções conhecidas para criar uma terceira solução, mais complicada, é conhecido como superposição.

Chamo atenção para o fato de que o conceito da superposição é útil, mas ele é válido somente para campos de escoamento irrotacional para os quais as equações para $\phi$ e $\psi$ são lineares. E sempre precisamos ter o cuidado de se certificar de que os dois campos de escoamento que queremos somar vetorialmente sejam ambos irrotacionais.

Superposição de dois campos de escoamento irrotacionais: $\>\>\> \phi = \phi_{1} + \phi_{2}$

Usando as equações de potencial de velocidade para escoamento irrotacional planar em coordenadas cartesianas, a componente $x$ da velocidade do escoamento composto é:

$$ u = \frac{\partial \phi}{\partial x} = \frac{\partial (\phi_{1} + \phi_{2})}{\partial x} = \frac{\partial \phi_{1}}{\partial x} + \frac{\partial \phi_{2}}{\partial x} = u_{1} + u_{2} $$

Podemos gerar uma expressão análoga para a componente $v$. Portanto, a superposição nos permite simplesmente adicionar as velocidades individuais vetorialmente em qualquer posição na região de escoamento, para obter a velocidade do campo de escoamento composto naquele posição.

Campo de velocidade composta resultante da superposição: $\overrightarrow{V} = \overrightarrow{V_{1}} + \overrightarrow{V_{2}}$

Agora que fizemos a matemática, é hora de exercitar nossos poderes de superposição e visualizar como são as linhas de correntes. Começamos adicionando esses campos de velocidade, de maneira inteligente, para obter uma nova solução de fluxo potencial, e assim conseguimos manipular diversos modelos clássico de fluxo.

2.1. Fonte e sumidouro de igual intensidade¶

Considere uma fonte $+m$ localizada em $(x, y) = (-a, 0)$, combinada com um sumidouro de igual intensidade $–m$, localizado em $(+a, 0)$, como na figura abaixo. A função corrente resultante é simplesmente a soma das duas. Em coordenadas cartesianas:

$$ \psi = \psi{_{fonte}} + \psi{_{sumidouro}} = m\tan^{-1}\left ( \frac{y}{x+a} \right ) + \left ( -m \right )\tan^{-1}\left ( \frac{y}{x-a} \right ) $$

De modo semelhante, o potencial de velocidades composto é:

$$ \phi = \phi{_{fonte}} + \phi{_{sumidouro}} = \frac{1}{2}m\ln \left [ \left ( x+a \right )^{2} + y^{2} \right ] + \frac{1}{2}\left ( -m \right )\ln \left [ \left ( x-a \right )^{2} + y^{2} \right ] $$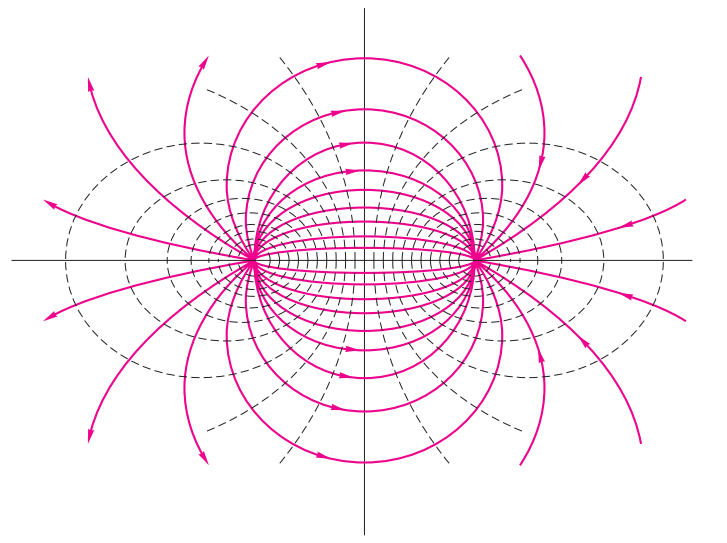

Utilizando identidades trigonométricas e logarítmicas, essas expressões podem ser simplificadas para:

$$ \psi = \psi{_{fonte}} + \psi{_{sumidouro}} = -m\tan^{-1}\left ( \frac{2ay}{x^{2} + y^{2} - a^{2}} \right ) $$ \phi = \phi{_{fonte}} + \phi{_{sumidouro}} = \frac{1}{2}m\ln \left [ \frac{\left ( x+a \right )^{2} + y^{2}}{\left ( x-a \right )^{2} + y^{2}} \right ] $$

Essas linhas estão representadas na figura cima, na qual se vê que são duas famílias de círculos ortogonais, com as linhas de corrente passando pelos locais da fonte e do sumidouro e as linhas equipotenciais circundando esses locais. Elas são funções harmônicas (laplacianas), exatamente análogas, na teoria eletromagnética, aos padrões de corrente elétrica e potencial elétrico de um ímã com polos em $(\pm a, 0)$.

Agora imagine que você está olhando para este padrão de fluxo de muito longe. As linhas de fluxo que estão entre a fonte e o coletor serão muito curtas, deste ponto de vista. E as outras linhas de fluxo começarão a parecer dois grupos de círculos, tangentes à origem. Se você olhar longe o suficiente, a distância entre a fonte e o dissipador se aproxima de zero, e o padrão que você vê é chamado de dipolo.

Embora o dipolo propriamente dito é gerado pela superposição de dois blocos básicos anteriores, isto é, uma linha de fonte e uma linha de sumidouro de intensidades iguais, sua formulação tem umas aproximações e sua formulação fica:

$$ \psi = -k\frac{\sin\theta}{r} \>\>\>\>\> \phi = k\frac{\cos\theta}{r} $$

Várias linhas de corrente e linhas equipotenciais para um dipolo estão mostradas na figura abaixo. Concluímos que as linhas de corrente são círculos tangentes ao eixo $x$, e as linhas equipotenciais são círculos tangentes ao eixo $y$. Os círculos interceptam-se em ângulos de 90° em todos os pontos exceto na origem, que é um ponto singular.

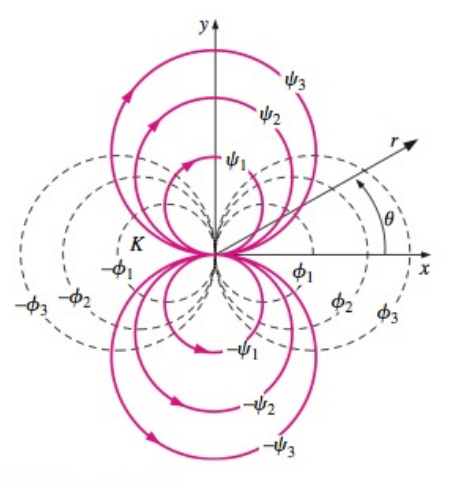
Se o k for negativo, o dipolo é "para trás", com o sumidouro localizado em $x=0^{2}$ (infinitesimalmente à esquerda da origem) e a fonte localizada em $x=0^{+}$ (infinitesimalmente à direita da origem). Nesse caso todas as linhas de corrente da figura acima seriam idênticas na forma, mas o escoamento seria na direção oposta.

2.2. Fonte (ou sumidouro) e vórtice na origem¶

Um padrão de escoamento interessante, aproximado na natureza, ocorre pela superposição de uma fonte e um vórtice, ambos centrados na origem. As funções corrente e potencial de velocidade compostas para uma fonte e vórtice são:

$$ \psi = m\theta - \frac{\Gamma}{2 \pi} \ln r \>\>\>\>\>\>\> \phi = m\ln r + \frac{\Gamma}{2 \pi} \>\theta $$

Quando traçadas, elas formam duas famílias de espirais logarítmicas ortogonais, como mostra a figura abaixo. Essa é uma simulação razoavelmente realista de um tornado (em que o escoamento do sumidouro, neste caso, se move para cima no eixo z e para dentro da atmosfera) ou então um “vórtice de ralo” com drenagem rápida.

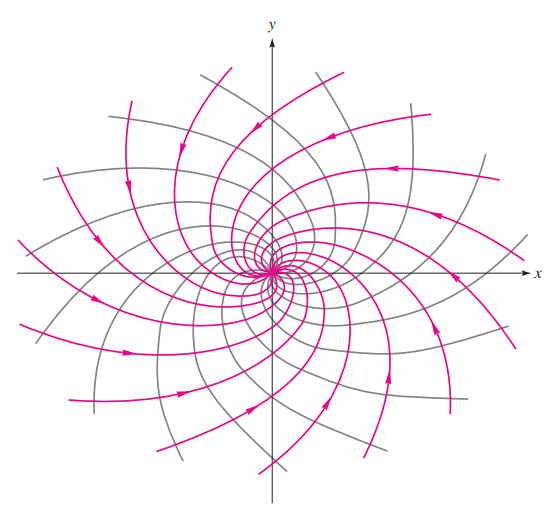
2.3. Corrente uniforme mais uma fonte na origem: o semicorpo de Rankine¶

Se fizermos a superposição de uma corrente uniforme na direção $x$ e de uma fonte, surge a forma de um semicorpo. Se a fonte está na origem, a função corrente composta é, em coordenadas polares:

$$ \psi = U\>r\sin\theta + m\>\theta $$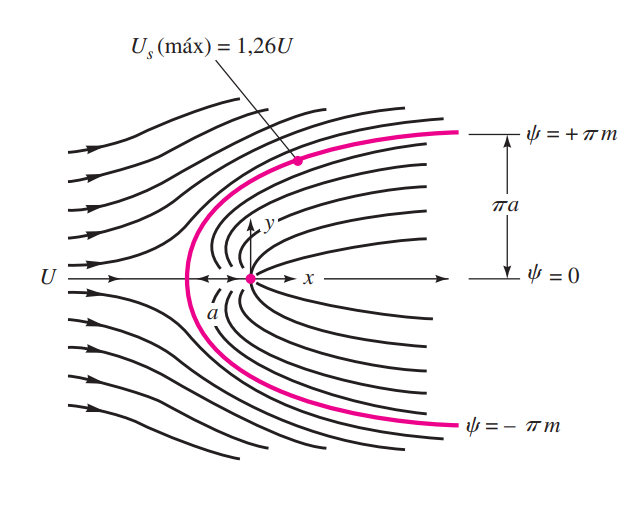

Aparece um semicorpo curvo, aproximadamente elíptico, que separa o escoamento da fonte do escoamento da corrente. A forma do corpo, cujo nome homenageia o engenheiro escocês W. J. M. Rankine (1820-1872), é formada pelas linhas de corrente particulares $\psi = \pm \pi m$. A semiespessura do corpo, bem a jusante, é $\pi m/U$. A superfície superior pode ser traçada pela relação:

$$ r = \frac{m(\pi - \theta)}{U \sin \theta} $$

Não se trata de uma elipse verdadeira. O nariz do corpo, que é um ponto de “estagnação”, em que $V = 0$, fica em $(x, y) = (-a, 0)$, em que $a = m/U$. A linha de corrente $\psi = 0$ também cruza esse ponto — relembre que as linhas de corrente podem se cruzar apenas em um ponto de estagnação.

2.4. Escoamento em torno de um vórtice¶

Considere uma corrente uniforme $U$ na direção $x$ escoando em torno de um vórtice de intensidade $K$ com centro na origem. Por superposição, a função corrente composta é:

$$ \psi = \psi_{corrente} + \psi_{vórtice} = U\>r\>\sin\theta - k\>\ln $$

As linhas de corrente estão traçadas na figura abaixo pelo método gráfico, interceptando as linhas de corrente circulares do vórtice com as linhas de corrente horizontais da corrente uniforme.

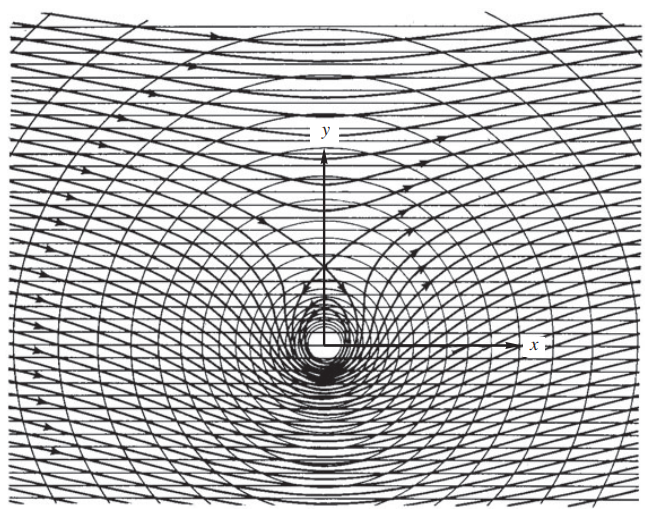
Provavelmente, a coisa mais interessante acerca deste exemplo é que existe uma força de sustentação não nula, normal à corrente, sobre a superfície de qualquer região envolvendo o vórtice, mas vamos adiar essa discussão para o próxima seção.

2.5. Uma fileira infinita de vórtices¶

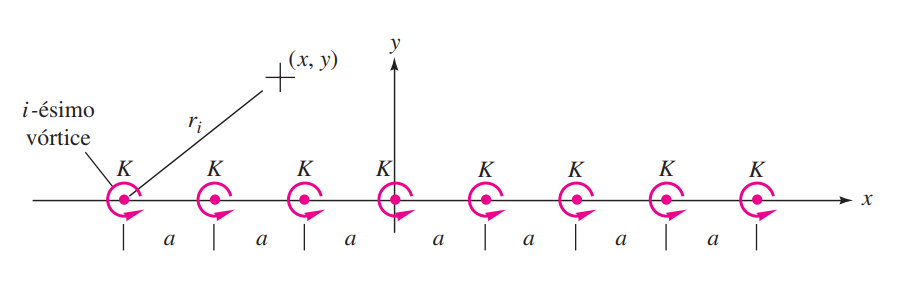
Considere uma fileira infinita de vórtices de mesma intensidade $K$ e mesmo espaçamento $a$, como na figura acima. Este caso é incluído aqui para ilustrar o interessante conceito de uma lâmina de vórtices, de modo que a fileira infinita completa tem uma função corrente composta:

$$ \psi = -k\sum_{i=1}^{\infty}\ln r_{i} $$

que essa soma infinita de logaritmos é equivalente a uma função em forma fechada,

$$ \psi = -\frac{1}{2}k\ln\left [ \frac{1}{2} \left ( \cosh \frac{2\pi y}{a} - \cos\frac{2\pi x}{a} \right ) \right ] $$

As linhas de corrente da equação acima estão traçadas na figura, mostrando aquilo que é chamado de padrão olho de gato, de células fechadas de escoamento em torno dos vórtices individuais. Acima dos olhos de gato o escoamento é todo para a esquerda e abaixo dos olhos de gato o escoamento é todo para a direita.

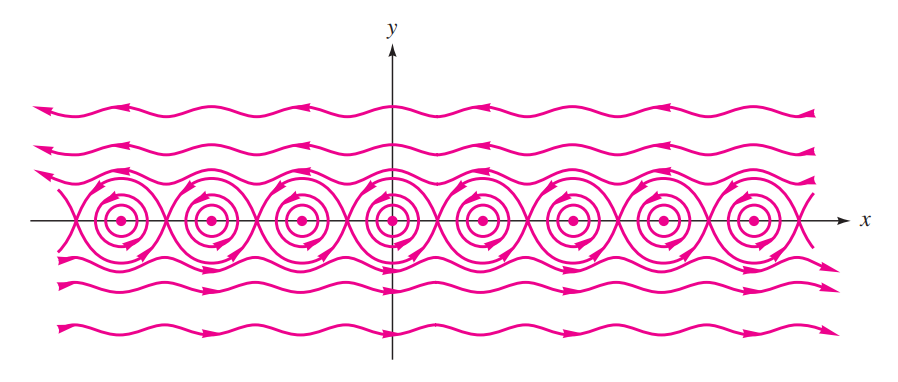
Além disso, esses escoamentos para a esquerda e para a direita tornam-se uniformes com $\left | y \right | \gg a$, o que decorre por diferenciação da equação acima:

$$ u = \left.\begin{matrix} \frac{\partial \psi}{\partial y} \end{matrix}\right| _{\left | y \right | \gg a} = \pm \frac{\pi k}{a} $$

em que o sinal de adição se aplica abaixo da fileira e o sinal de subtração, acima da fileira. Ressalto que esse efeito é induzido pela fileira de vórtices: não há corrente uniforme aproximando-se da fileira neste exemplo.

2.6. A oval de Rankine¶

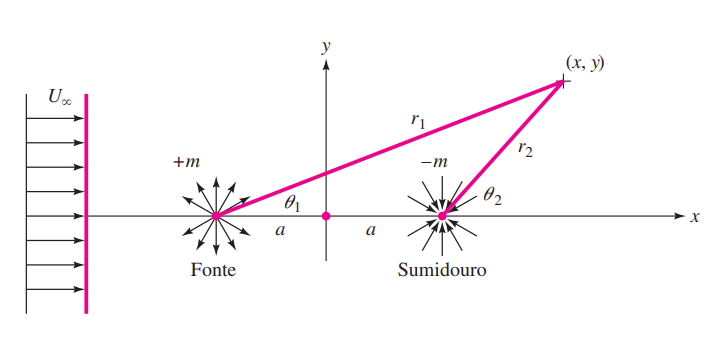
Um formato cilíndrico chamado oval de Rankine, que é longo em comparação com sua altura, é formado por um par fonte-sumidouro alinhado com uma corrente uniforme, como na figura acima, das equações das soluções base, a função corrente composta é:

$$ \psi = U\>y - m \tan^{-1}\frac{2ay}{x^{2} + y^{2} - a^{2}} = U\>r\sin\theta + m(\theta_{1} - \theta_{2}) $$

Quando as linhas de corrente são traçadas por meio da equação acima, um formato de corpo oval aparece, como na figura abaixo. O semicomprimento $L$ e a semialtura $h$ da oval dependem da intensidade relativa da fonte e da corrente, isto é, da razão $m/(Ua)$, que é igual a $1.0$ no exemplo. As linhas de corrente circulantes no interior da oval não têm interesse e costumam não ser mostradas. A oval é a linha $\psi = 0$.

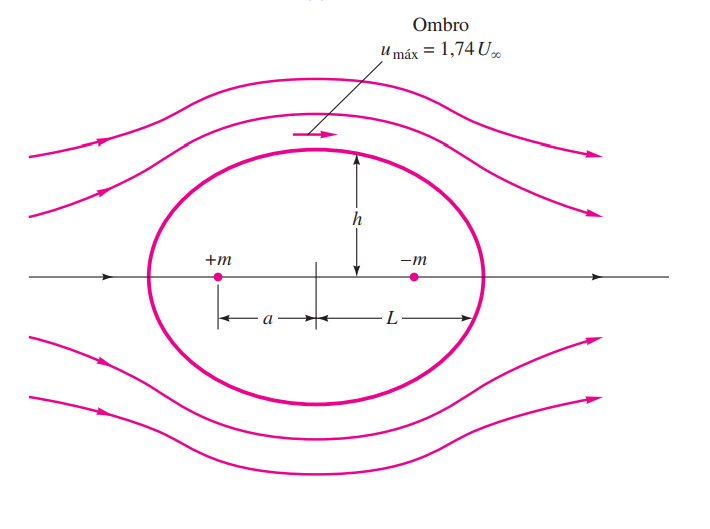
À medida que aumentamos $m/(U a)$ desde zero até grandes valores, o formato da oval cresce em tamanho e espessura desde uma placa plana de comprimento $2a$ até um cilindro bem grande, quase circular. Isso está na tabela a seguir. No limite com $m/(U a) \rightarrow \infty, L/h \rightarrow 1.0$ e $u_{max}/U_{infty} \rightarrow 2.0$, o que equivale ao escoamento em torno de um cilíndrico circular.

$m/(U_{\infty}a)$	$h/a$	$L/a$	$L/h$	$u_{max}/U_{\infty}$
0.000	0.0000	1.0000	$\infty$	1.000
0.010	0.0310	1.0100	32.79	1.020
0.100	0.2630	1.0950	4.169	1.187
1.000	1.3070	1.7320	1.326	1.739
10.00	4.4350	4.5830	1.033	1.968
100.0	14.130	14.177	1.003	1.997
$\infty$	$\infty$	$\infty$	1.000	2.000

Todas as ovais de Rankine, exceto aquelas bem delgadas, têm um forte gradiente de pressão adverso em sua superfície posterior. Assim, a separação de camada-limite irá ocorrer na traseira seguida de uma larga esteira descolada, e o padrão não viscoso não será realista nessa região.

2.7. Escoamento em torno de um cilindro circular com circulação¶

Da tabela do item $2.6$, para grandes intensidades da fonte, a oval de Rankine torna-se um grande círculo, com diâmetro muito maior que o espaçamento $2a$ entre a fonte e o sumidouro. Visto da escala do cilindro, isso é equivalente a uma corrente uniforme mais um dipolo. Adicionando também um vórtice no centro do dipolo, o que não altera o formato do cilindro.

Logo, a função corrente para o escoamento em torno de um cilindro circular com circulação, centrado na origem, corresponde a uma corrente uniforme mais um dipolo mais um vórtice:

$$ \psi = U_{\infty}\sin\theta\left ( r - \frac{a^{2}}{r} \right ) - k\>\ln\frac{r}{a} $$

As linhas de corrente estão traçadas na figura abaixo para quatro valores diferentes da intensidade adimensional do vórtice $K/(U_{\infty}a)$. Em todos os casos, a linha $\psi = 0$ corresponde ao círculo $r = a$, isto é, o formato do corpo cilíndrico. À medida que a circulação $\Gamma = 2\pi K$ aumenta, o escoamento torna-se mais e mais rápido abaixo do cilindro e mais e mais lento acima dele.

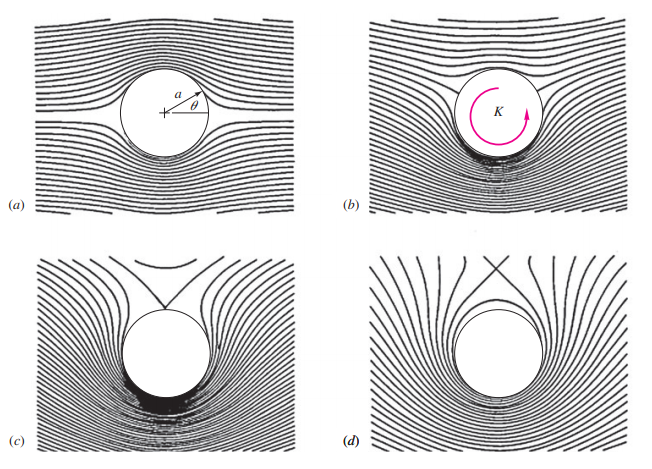
A figura (a) acima é para $K = 0$, $\theta_{e} = 0°$ e $180°$, isto é, escoamento não viscoso duplamente simétrico em torno de um cilindro circular sem circulação. A figura (b) é para $K/(U_{\infty} a) =1$, $\theta_{e} = 30°$ e $150°$ e a figura (c) é o caso-limite em que os dois pontos de estagnação se encontram no topo, $K/(U_{\infty} a) = 2$, $\theta_{e} = 90°$. Para $k > 2U_{\infty}a$, a equação acima não é valida e o único ponto de estagnação ocorre acima do cilindro, como na figura (d), em um ponto $y= h$ dado por

$$ \frac{h}{a}=\frac{1}{2}\left [ \beta^{2} + (\beta^{2} - 4) ^ {1/2} \right ] \>\>\>\>\>\>\>\> \beta = \frac{k}{U_{\infty}a}, $$

na figura (d), $k/(U_{\infty}a) = 3.0$ e $h/a = 2.6$ .

2.8. A oval de Kelvin¶

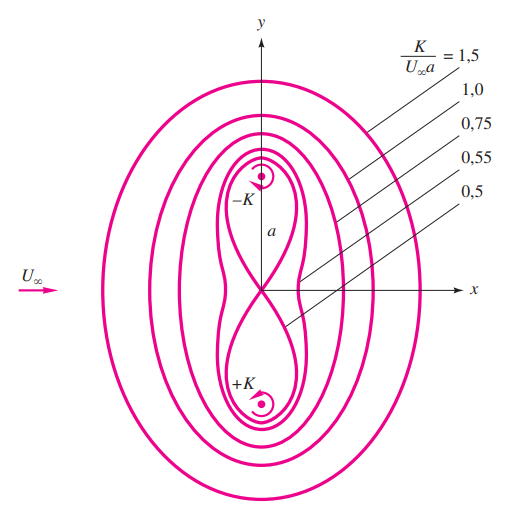
Uma família de formatos de corpos mais altos do que largos pode ser formada considerando-se uma corrente uniforme normal a um par de vórtices. Se $U_{\infty}$ for para a direita, o vórtice negativo $\pm K$ é colocado em $y = -a$ e o vórtice anti-horário $+K$ é colocado em $y = –a$, como na figura acima. A função corrente composta é:

$$ \psi = U_{\infty} y - \frac{1}{2}k\ln\frac{x^{2}+(y+a)^{2}}{x^{2}+(y-a)^{2}} $$

O formato do corpo corresponde à linha $\psi = 0$, e alguns desses formatos estão na figura acima. Para $K/(U_{\infty} a) > 10$, o formato fica a menos de 1% de uma oval de Rankine girada a $90°$, mas para valores pequenos de $K/(U_{\infty}a)$, a cintura fica comprimida e uma figura em formato de oito aparece para $K/(U_{\infty} a) = 0.5$, para $K/(U_{\infty} a) < 0.5$, a corrente flui para a direita entre os vórtices, isolando dois formatos de corpo mais ou menos circulares, cada qual envolvendo um vórtice.

Um corpo fechado de formato praticamente arbitrário pode ser construído pela superposição adequada de fontes, sumidouros e vórtices. Consulte trabalhos mais avançado na literatura para detalhes adicionais.